Teorema lui Ceva, metoda eleganta de demonstrare a concurentei liniilor importante in triunghi

Elemente teoretice asupra concurenţei:
Definiţie: Dreptele d1, d2,…,dn, nN\{0,1} se numesc concurente, daca toate trec prin acelaşi punct.
Observaţia 1: Cazul trivial este cel in care n=2, deoarece doua drepte distincte d1 si d2 situate in acelaşi plan si nu sunt paralele, se intersectează intr-un punct. Cazurile interesante sunt cele in care n N\{0,1,2}.
Comentariu: Intre problemele de concurenta si cele de coliniaritate este o strânsă legătură. Astfel pentru a dovedi ca dreptele d1, d2 si d3 sunt concurente, se considera punctul P comun dreptelor d1 si d2 precum si punctele M si N situate pe dreapta d3. atunci problema iniţială se reduce la a arata ca punctele M, N, P sunt coliniare.
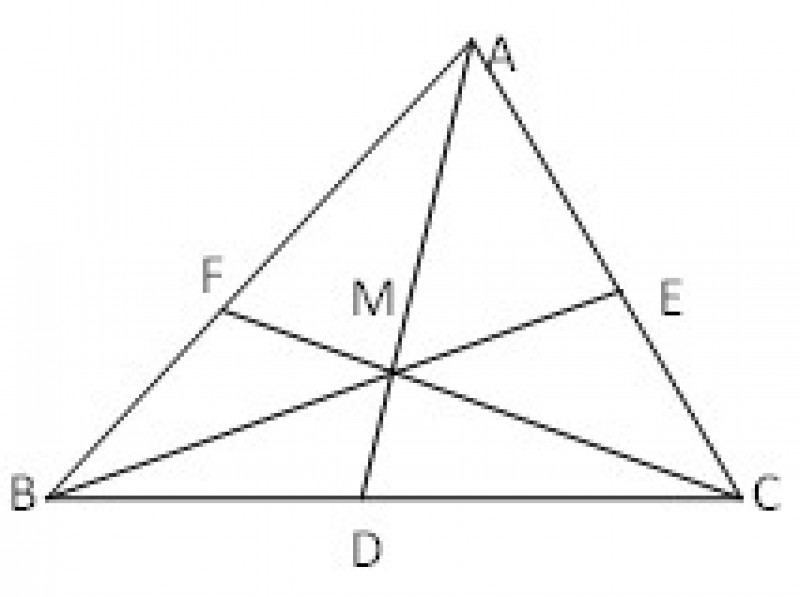
Definiţie: Ceviana intr-un triunghi este dreapta determinata de un vârf al acestuia si un punct pe latura opusa.
Teorema lui Ceva: AD,BE, CF sunt ceviene concurente in triunghiul ABC, daca si numai daca este adevărata egalitatea: AF/FB*BD/DC*CE/EA=1
Soluţia 1:
Fie M punctul de concurenta al cevienelor BE, AD, CF. Aplicând teorema lui Menelaus in triunghiul BEC si transversala AMD, apoi aplicand relaţia lui Menelaus in triunghiul ABE si transversala CMF, se obtin produse de rapoarte egale cu 1. Inmultind cele doua relatii se obtine relatia lui Ceva.
Observaţia 2: Teorema este valabila si daca punctele D,E,F sunt situate pe dreptele suport ale laturilor triunghiului, in exteriorul acestuia.
Solutia 2: Se aplica rezultatul care afirma ca „ daca P este un punct pe baza BC a triunghiului oarecare ABC, atunci segmentele PB si PC sunt proporţionale respectiv cu ariile triunghiurilor APB si APC”
Reciproca teoremei lui Ceva se demonstreaza prin reducere la absurd
Daca D, E, F sunt trei puncte situate pe BC, AC respectiv AB si este verificata relaţia (1) atunci dreptele AD, BE, CF sunt concurente.
Intr-adevăr deoarece D si F aparţin dreptelor BC si AB si cum BC si AB nu sunt paralele rezulta ca ele se intersectează intr-un punct M.
Presupunând ca M nu aparţine lui BE, atunci BM intersectează AC intr-un punct E’.Aplicând relaţia lui Ceva in triunghiul ABC pentru cevienele concurente AD, CF si BE’ rezulta prin inmultirea rapoartelor valoarea 1.
Observaţie: Reciproca teoremei lui Ceva este o metoda puternica si eleganta de demonstrare a concurentei a trei drepte.
Teorema (concurenţa bisectoarelor): Intr-un triunghi oarecare bisectoarele interioare sunt concurente. Se demonstreaza cu ajutorul teoremei bisectoarei pentru cele trei bisectoare, apoi inmultind rapoartele membru cu membru, obtinem relatia lui Ceva, deci concurenta bisectoarelor este astfel demonstrata.
Teorema:(concurenţa medianelor) Intr-un triunghi oarecare medianele sunt concurente. Demonstratie simpla AF/FB*BD/DC*CE/EA=1 deoarece in acest caz F,D, E sunt mijloacele laturilor triunghiului ABC.
Teorema (concurenta inaltimilor unui triunghi): Intr-un triunghi înălţimile sunt concurente. Pentru demonstratie se aplica asemanarea triunghiurilor dreptunghice (de exemplu ADC si BEC), apoi se inmultesc relatiile obtinute din asemanare de unde rezulta relatia lui Ceva, deci concurenta inaltimilor.
Concluzie:Teorema lui Ceva, sau Teorema lui Menelaus permit demonstratii elegante ale problemelor care concluzioneaza concurente sau coliniaritati.