Contribuţii româneşti la dezvoltarea ştiinţei şi tehnicii
Galerie foto
Vor fi inserate cele mai sugestive imagini ale proiectului.
Matematicienii



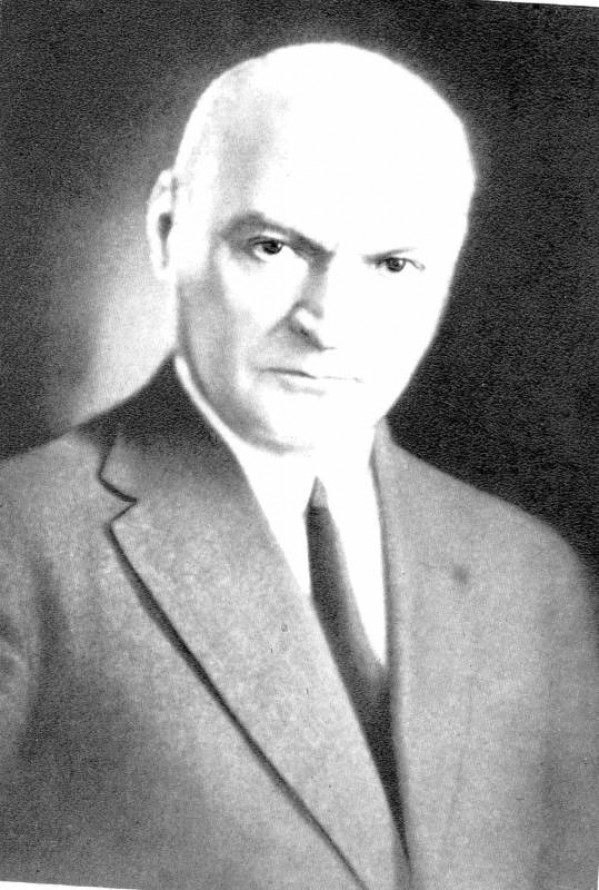




Propus de: iulianasweety50 | 11.12.2013 16:26
Dimitrie Pompeiu

Propus de: CatanoiuDaniel1 | 10.12.2013 17:58
Ernest Abason; Dan Barbilian;


Propus de: CatanoiuDaniel1 | 10.12.2013 17:51
Nicolae Teodorescu

Propus de: CatanoiuDaniel1 | 10.12.2013 17:45
Documentare privind domeniul matematic
Documente privind domeniu matematic
Instrucţia şi creaţia matematică sunt strâns legate de existenţa unui sistem organizat de învăţământ, care asigură climatul de formare a îndrumătorilor şi a viitoarelor valori.
În secolul XIX-lea, în ţările române au început să funcţioneze şcoli care formau învăţători şi profesori - cadre ce urmau să aibă un rol hotărâtor în dezvoltarea potenţialului de creaţie şi în domeniul matematicii. După planul conceput de Veniamin Costache, în 1820 începe să funcţioneze Seminarul de la Socola, în al cărui plan de învăţăãmânt erau prevăzute şi ore de matematică.
La Arad, funcţiona încă din 1812 şcoala Pedagogică, numită atunci Preparandia - cea mai veche şcoală normală din România. Şcoala de la Socola şi clasa de inginerie de la Şcoala Domnească din Iaşi, organizată de Gheorghe Asachi (1788-1869), au marcat dezvoltarea ulterloară a vieţii ştiinţifice în învăţământul şi cultura românească. În Ţara Românească, din 1818 a început să funcţioneze Şcoala de la “Sf Sava"- organizată de Gheorghe Lazăr (1779-1823). Manualele de matematică utilizate la început (1830) erau doar transcrieri după autori celebri: algebra lui Bézout ori geometria lui Legendre. Manualele de matematici de învăţământ superior, elaborate de autori români, încep să apară la mijlocul secolului al XIX-lea. Menţionăm “Cursul de geometrie descriptivă” (1851), elaborat la Bucureşti de Alexandru Orăscu (1817-1894), “Lectii de calcul diferenţial şi integral” (1870) elaborat la laşi de Neculai Culianu.
Paralel cu activitatea didactică, se manifestă de timpuriu şi o interesantă activitate de creaţie matematică. Astfel, la Târgu Mureş a apărut una dintre cele mai originale şi surprinzătoare personalităţi ale geometriei, care va răsturna imaginea clasică oficializată până atunci în întreaga Europă şi a cărei contribuţie o vom prezenta în viitorul capitol. Alături de el, putem măcar cita pe Dimitrie Arachi (1820-1868), care elaborează şi tipăreşte la München prima lucrare originală de matematică privind inversarea seriilor.
Janos Bolyai, un reformator al geometriei
Unui geometru născut în Targu Mureş, care - asemenea multora dintre genii - a avut parte în timpul vieţii de sărăcie lucie şi de neînţelegerea şi ingratitudinea contemporanilor, iar moartea i-a fost consemnată ca un fapt divers întâmplat unui om despre care cartea matricolă a bisericii reformate consemna lapidar că “viaţa i s-a scurs fără niciun rost”, i-a fost sortit să răstoarne marile adevăruri ale Antichităţii şi să dea o nouă viziune geometriei lui Euclid.
E vorba de Janos Bolyai care, aproape simultan şi absolut independent de rusul Lobacevski, a realizat - după afirmaţiile lui Clifford, unul dintre cei mai mari matematicieni ai lumii – “o nouă revoluţie coperniciană în concepţia noastră despre Univers”.
Deşi ofiţer la Direcţia Fortificaţiilor din Timişoara, marea lui pasiune, care-i ocupa tot timpul, erau matematicile, în special celebra problemă a paralelelor care nu se pot întâlni niciodată şi nicăieri, după concepţiile neclintite de două milenii.
În 1825, îşi sistematizează rezultatele într-o mică lucrare pierdută ca şi lucrarea din 1829 a lui Lobacevski, fiind tipărită abia în 1831, la Târgu Mureş, sub titlul generic de “Ştiinţa absolută a spaţiului” şi convenţional de “Appendix”.
Ca şi Lobacevski, Bolyai nu a avut parte de satisfacţia recunoaşterii valabilităţii ideilor sale în cursul vieţii. Mai târziu, datorită lucrărilor profesorului de la Göttingen, Bernhard Riemann - el însuşi nerecunoscut în timpul vieţii -, ideile celor doi matematicieni revoluţionari încep să învingă o prejudecată seculară.
Abia peste un veac, când Albert Einstein, în revoluţionara sa teorie a relativităţii (despre care acum sunt destule teorii care ne demonstrează inexactitatea ei), a descoperit că drumurile pe care se propagă lumina în spaţiul cosmic formează o familie de drepte neeuclidiene, s-a convenit că doar teoria lui Bolyai-Lobacevski permite înţelegerea deplină a structurii Universului. Pornind de la ideea că “legea gravitaţiei pare a fi într-o strânsă legătură cu forma, cu esenţa, cu felul de a fi al spaţiului”, s-a demonstrat că, sub raport matematico-astronomic, geometria Universului este neeuclidiană, infirmând radical mecanica lui Newton, deoarece pot apărea abateri esenţiale în traiectoria planetelor, iar spaţiul nu poate fi despărţit de materie. Această idee a fost confirmată în mod strălucit când în mişcarea planetei Mercur a fost observată o abatere sistematică de la traiectoria newtoniană, abatere ce nu putea fi explicată decât cu ajutorul teoriei relativităţii, care se bazează pe geometria neeuclidiană.
Înlocuirea fixismului newtonian cu dialectica einsteiniană confirmată de cercetärile lui Bolyai şi Lobacevski a deschis noi zări ştiinţei matematice a Universului şi a constituit o valoroasă contribuţie românească la dezvoltarea modernă a unor discipline fundamentale.
Un erudit şi multilateral matematician: Emanoil Bacaloglu
Primul savant de factură enciclopedică al României a fost Emanoil Bacaloglu (1830-1891), specialist egal de valoros în trei mari domenii: matematici, fizică şi chimie (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 26, din acest forum). În 1856 pleacă la Leibnitz, unde studiază matematicile cu celebrul Moebius, fizica cu Hankel şi chimia cu Erdmann. În anul 1857 îl găsim la Paris, unde publică trei lucrări originale de matematici, dintre care una avea să fie înscrisă în cartea de onoare a acestei ştiinţe.
Pentru prima oară aduce o importantă ameliorare a problemei curburii suprafeţelor găsind o formulă nouă care măsoară curbura unei suprafeţe într-un punct al ei.
În lucrarea clasică privind suprafeţele curbe apărută în 1828, Gauss a dat a formula celebră a curburii totale a suprafeţei:
Ctot= 1/(R1R2)
unde R1 si R2 sunt valorile razelor principale de curbură ale unei suprafeţe. Gauss a arătat că rezultatul rămâne acelaşi dacă încovoiem suprafaţa fără a o dilata sau contracta. Aceasta înseamnă că o suprafaţă desfăşurabilă pe un plan (cilindru sau con) are o curbură nulă. Măsura gaussiană a curburii nu ne dă însă posibilitatea să distingem, pe baza comportamentului suprafeţei într-un punct al ei, între suprafeţe care au aceeaşi curbură totală, de exemplu con, cilindru şi plan.
Remarcând această carenţă, Bacaloglu a propus următoarea formulă:
C=1/((R1+R2)/2 √(R1 R2 ))
(pentru o citire corectă a formulelor trebuie consultată cartea deoarece acest editor nu permite redactarea corectă)
El consideră acţiunile normale prin punctul dat, dar nu cu ajutorul normalelor de suprafaţă, ci cu ajutorul normalelor la curbele plane ale acestor secţiuni. Formula lui a fost adoptată în geodezie.
După numirea în 1861 ca profesor de fizică la Universitatea din Bucureşti, el se ocupă de problemele iluminatului electric aflat în Romania la începuturile lui şi organizează primul laborator modern de şcoală, unde s-a format tânăra pleiadă de cercetători care aveau să se afirme în deceniile următoare.
El n-a neglijat nici preocupările din domeniul chimiei – publicând, între 1860 şi 1864, câteva lucrări valoroase în diferite reviste de specialitate de peste hotare (“Les Mondes”, “Jurnal fur practiche Chemie”, ”Cosmos”), ceea ce demonstrează formaţia şi preocupările enciclopedice, anticipând viziunea interdisciplinară a învăţământului contemporan.
Explozia creatoare a matematicii.Prima generaţie de nume ilustre
După mijlocul secolului al XIX-lea începe o puternică înflorire a matematicilor româneşti, numărul profesorilor şi cercetătorilor de valoare internaţională începând să crească simţitor odată cu apariţia unor facultăţi prestigioase, a unor centre de cercetare şi datorită închegării unor puternice şcoli, care vor da numeroase generaţii de specialişti. După 1944 tradiţia matematică românească primeşte o confirmare internaţională, întărită continuu după înfiinţarea în 1949 a Institutului de matematica al Academiei Romane. În afara numeroaselor doctorate în ţară şi străinătate care primesc confirmăări internaţionale, publicaţiile matematice care şi-au păstrat o exemplară continuitate au contribuit masiv la afirmarea viitorilor matematicieni şi la o largă popularitate a acestei discipline fundamentale, universal aplicate şi aplicabile. Cităm printre altele “Recreaţii ştiinţifice”, din Iaşi, şi mai ales “Gazeta matematică” (funcţionand continuu pană azi), apărută la Bucureşti.
Prima generatie înscrie în cartea de aur a matematicii româneşti o trinitate de valoare internaţională: David Emmanuel, Gheorghe Ţiţeica, Dimitrie Pompeiu.
David Emmanuel, “savantul înţelept, de o modestie sinceră şi statornică, model de iubire a ştiinţei şi a studenţilor”, cum îl caracteriza în 1929 profesorul E.A. Pangrati, poate fi considerat întemeietorul şcolii matematice româneşti.
Ca 90% dintre marile personalităţi ale României, care au pornit de jos, din păturile populare de la sate şi oraşe, au cunoscut dramatic sărăcia şi lipsurile, dar şi-au învins condiţia umilă prin talent, muncă şi perseverenţă, şi David Emmanuel şi-a împlinit visul şi destinul.
Din economille unei munci dure, a plecat la Paris, unde rămane 6 ani trăind din meditaţii, urmând Facultatea de Matematică a Universităţii din Sorbona, iar în 1879, în faţa unui juriu din care făcea parte marele matematician Briot, îşi susţine o strălucită teză de doctorat cu subiectul “Studii asupra integralelor abeliene de speţă a III-a”, care-şi păstrează şi azi actualitatea.
A refuzat propunerea de a rămâne în Franţa şi, întors în ţară, este numit profesor universitar. El este acela care a introdus matematicile superioare în învăţământul universitar ştiinţific şi tehnic (a fost profesor şi la “Şcoala de poduri şi şosele”), formând cincizeci de promoţii din care s-au evidenţiat matematicieni de frunte, cunoscuşi şi peste hotare, de la Gheorghe Ţiţeica şi Dimitrie Pompeiu, până la Grigore Moisil şi Gheorghe Mihoc. “El a introdus şi a revoluţionat pe alocuri - cum recunoştea Gheorghe Ţiţeica – “teoria funcţiilor” şi în special a funcţiilor eliptice şi modulare, cursul său fiind considerat unul dintre cele mai desăvârşite tratate din literature mondială asupra acestei chestiuni”.
Elev al lui David Emmanuel, Gheorghe Ţiteica (1873-1939) are meritul de a fi creatorul şcolii româneşti de geometrie diferenţială modernă. Fiul unui mecanic de vapor, el face liceul la Craiova, îşi la licenţa în matematici la Bucureşti, pleacă apoi în Franţa în 1898, îşi susţine doctoratul la Sorbona cu tema: “Asupra congruenţelor ciclice si asupra sistemelor triplu conjugate” cu Henri Poincarl şi Gaston Darboux, maestrul său.
Numit profesor de geometrie analitică la Bucureşti, este ales în 1913 membru al Academiei Romane şi se face cunoscut pe plan internaţional prin lucrările de geometrie diferenţială, considerate clasice, noţiunea de suprafeţele lui Ţiţeica” (descoperite de el în 1906) intrând în terminologia matematică universală. Aceste suprafeţe au căpătat ulterior denumirea de “sfere centroafine” - deschizand un nou domeniu de geometrie. Există şi o familie de curbe denumite “Curbele lui Ţiţeica” şi o clasă de reţele” care-I poartă de asemenea numele.
El este primul şi cel mai mare popularizator al matematicii la noi, prin revista “Gazeta matematicii” şi celebrul concurs şcolar de matematici, care, iniţiate în 1913 şi perpetuate pană în prezent, au trezit interesul tineretului pentru această disciplină, făcând din România unul dintre centrele de radiere mondială a matematicii, iar prin “olimpiadele” şcolare de matematică din prezent, una dintre ţările fruntaşe în acest domeniu (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 2, din acest forum).
Dimitrie Pompeiu, al treilea stâlp al primei generaţii de mari matematicieni, s-a născut în 1873 în satul Broscăuţi din Botoşani şi, ca toţi savanţii noştri cu origine modestă, şi-a croit cu greu drumul în viaţă, evoluând prin muncă de la un simplu institutor la un strălucit student şi doctorand la Sorbona. În 1905 îşi susţine teza de doctorat, sub conducerea celebrului profesor H. Poincaré, în dificila problemă a aşa-numitelor funcţii analitice. Aici el a demonstrat existenţa funcţiilor analitice uniforme şi continue pe mulţimea singularităţilor, teză confirrnată şi apoi reluată de mari savanţi din întreaga lume şi omologată în 1909, Pompeiu devenind un deschizător de drumuri în acest domeniu (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 10, din acest forum).
Tot el se remarcă şi prin descoperiri însemnate în direcţia funcţiilor de o variabilă complexă şi de o variabilă reală şi contribuţii originale în teorema creşterilor finite legate de geometria triunghiului. Noţiunea de derivată areolară” este una dintre cele mai importante noţiuni introduse de el în matematică şi a fost dezvoltată ulterior de reprezentanţii celei de a doua generaţii importante de matematicieni, printre care Miron Nicolescu, C. Călugăreanu, Grigore Moisil, Nicolae Teodorescu.
Ca răsplată a meritelor sale, a fast ales in 1934 academician, iar numele lui a fost dat Institutului de Matematică al Academiei Romane.
Jurjiu Gheorghe
A doua “invazie” victorioasă a marilor matematicieni
A doua generaţie de mari matematicieni îşi face simţită prezenţa pe plan naţional şi internaţional de-a lungul secolului al XX-lea, în două reprize, fiind în mare parte constituită din elevi şi discipoli ai savanţilor din prima generaţie. Numărul lor este impozant şi ne obligă la o selecţie nedreaptă poate cu nume care ar merita din plin să fie citate.
În prima etapă, autoritatea mondială este profesorul şi academicianul român Traian Lalescu (1882-1929). Bănăţean, el îşi face iniţial studille în patrie, apoi pleacă în ţara visată de taţi romanii, în 1905, şi-şi dă doctoratul în matematici la Paris cu o teză privind ecuaţiile integrale Volterra, savant pe care îl preţuia şi care la rândul său i-a arătat o mare prietenie. În numai doi ani (1907-1908) publică 14 memorii pe care le va cuprinde în volumul “Introducere la teoria ecuaţiilor integrale”, lucrare fundamentală în această ramură matematică, la fel de actuală şi în zilele noastre.
A depus mari strădanii pentru înfiinţarea, în 1920, a Şcolii Politehnice din Timişoara, al cărei director a fost pană la moartea sa, în floarea vârstei (47 de ani), deplânsă de toţi matematicienii (alte date se pot găsi şi în secţiunea “Biografiile unor mari români”
Theodor Angheluţă (1882-1964) a adus contribuţii notabile în studiul seriilor trigonometrice, al funcţiilor reale, al ecuaţiilor diferenţiale, integrale, funcţionale şi algebrice, iar Aurel Angelescu (1866-1938), doctor la Sorbona în 1916, a generalizat polinoamele lui Legendre şi Hermite, ocupându-se de funcţiile generatoare ale claselor de polinoame. În literatura de specialitate se vorbeşte de “polinoamele Angelescu”.
În domeniul pasionant al geometriei diferenţiale, doctorul în matematici de la Göttingen, Alexandru Myller (1879-1965), a jucat un rol activ, fiind primul matematician român care a studiat ecuaţii integrale cu nuclee simetrice. În 1912 înfiinţează Seminarul matematic al Universităţii din Iaşi, inaugurând cursul de geometrie diferenţială şi abordand o variată tematică matematică. Soţia sa, Vera Myller-Lebedev (1880-1970), a fost prima femeie profesoară universitară de matematici şi a avut contribuţii citabile la teoria ecuaţiilor integrale şi la teoria funcţiilor analitice.
O a doua etapă ni-i pune în faţă pe matematicienii născuţi şi afirmaţi mai ales după al Doilea Război Mondial şi în anii dictaturii comuniste.
Numărul lor creşte considerabil şi acoperă tot mai dens harta preocupărilor matematice din ce în ce mai complexe şi diversificate.
Octav Onicescu (1892-1976) a predat primul curs de teoria probabilităţilor în Romania, introducând în 1935 noţiunea de lanţ legături complete, pe cea de energie informaţională, de funcţie olotropă etc. (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 16, din acest forum).
Dan Barbilian (cu pseudonimul poetic de Ion Barbu), născut în 1893 şi mort în 1961, este unul din marii geometri ai ţării. S-a ocupat de axiomatizarea geometriei şi a mecanicii şi a adus contribuţii valoroase în geometria algebrică şi teoria grupurilor, inelelor şi idealurilor (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 8, din acest forum).
Ernest Abason (1897-1942) este unul dintre primii autori care, pe plan mondial, s-au ocupat de unele aspecte ale funcţiilor spline periodice, iar Miron Nicolescu (1903-1977) are contribuţii fundamentale în teoria funcţiilor poliarmonice, teoria funcţiilor policalorice, teoria măsurii Jordan, teoria funcţiilor areolar-conjugate, fiind creatorul şcolii româneşti de analiză modernă.
De un deosebit prestigiu s-a bucurat profesorul academician Simion Stoilov (1887-1961), doctor în matematici la Sorbona cu un subiect privind “clasele de funcţii de două variabile” definite prin ecuaţii liniare cu derivate parţiale. Se impune pe plan mondial prin lucrările sale ulterioare privind proprietăţile topologice ale funcţiilor analitice de variabilă complexă, devenind astfel fondatorul unui nou capitol al analizei matematice. Şcoala românească de teoria funcţiilor, pe care el a fondat-o, este de notorietate mondială.
“Transformările interioare”, introduse de marele matematician în ştiinţă în 1928, constitule azi noţiuni de bază în domeniul topologiei sau al funcţiilor complexe şi i-au permis lui Stoilov să aprofundeze valorile excepţionale şi asimptotice ale funcţiilor analitice, să introducă noi concepte, să ofere o serie de noi demonstraţii. Tot pornind de la transformările interioare, savantul a rezolvat o problemă fundamentală a teoriei funcţiilor analitice: definirea suprafeţelor riemanniene de acoperire; astfel a fost creat un nou şi important domeniu de cercetare.
Opera sa fundamentală e cuprinsă în două lucrări intrate în clasicitate: “Leçons sur les principes topologiques de la théorie des fonctions analytiques” (1938) şi “Teoria funcţiilor de o variabilă complex” (1959).
Nicolae Teodorescu (1908-2002), academician, a introdus printre altele funcţiile monogene (a) şi olomorfe (a) şi a dezvoltat teoria geometrică a ecuaţiilor diferenţiale sau cu derivate parţiale.
George Călugăreanu (1902-1976), academician, are temeinice contribuţii în teoria funcţiilor de variabilă complexă, teoria invarianţilor, geometria diferenţială şi topologie, adeseori citate.
Desi reputat astronom, Constantin C. Popovici (1878-1956) a debutat în ştiinţă ca matematician, fiind declarat doctor la Sorbona cu teza: “Sur les surfaces intégrales communes des équations differentielles” (1909). În sectorul matematicii el s-a consacrat mai ales problemelor de analiză matematică, oferind contribuţii de seamă în studiul ecuaţiilor integrale, integro-diferenţiale şi funcţionale.
Gheorghe Mihoc (1906-1994), intemeietorul Şcolii de Statistică Matematică din România, a introdus alături de Octav Onicescu lanţurile cu legături complete şi a aplicat teoria proceselor stocastice în asigurări.
Tiberiu Popovici (1906-1975) a contribuit la întemeierea şcolii clujene de calcul numeric, conducând Institutul de Calcul Numeric, fondat în 1957, unde s-au realizar în 1966 calculatoarele digitale româneşti.
Om de mare cultură şi inteligenţă scăpărătoare, acad. Grigore C. Moisil (1906-1973) introduce în mecanica continuă noţiunea de sisteme continue olonome, aplică metodele algebrei moderne la unele clase de ecuaţii cu derivate parţiale, extinde derivata areolară la spaţiul cu multe dimensiuni, utilizează pentru prima oară în lume algebrele trivalente şi polivalente, scrie lucrări importante în logica matematică şi e considerat un pionier al aplicării metodelor funcţionale în mecanică şi geometrie diferenţială.
Alături de Dan Barbilian, profesorul dr. Gheorghe Vrânceanu (1900-1979) este apreciat ca fiind cel mai important geometru contemporan. A creat la 26 de ani teoria spaţiilor neolonome şi a avut numeroase contribuţii fundamentale în diverse capitole ale geometriei diferenţiale contemporane, în domeniul spaţiilor cu diferite tipuri de conexiune, în domeniul grupurilor Lie, al varietăţilor diferenţiale, inclusiv numeroase contribuţii privind relativitatea (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 16, din acest forum).
O distinsă profesoară de matematici, dr. Florica Câmpan (1906-1988) a fost cunoscută ca geometră, istoric al matematicii şi cea mai cunoscută şi apreciată popularizatoare a matematicii în rândul elevilor şi tineretului, cărţile ei bucurându-se de o largă difuziune chiar şi internaţională (ca a matematicianului rus Perelman).
Trei academicieni împlinesc în ultimele decenii vârfurile performanțelor științifice ale matematicii românești. E vorba de Grigore Moisil (alte date se pot găsi şi în secţiunea “Biografiile unor mari români” la pagina 25, din acest forum)., Gheorghe Motoc şi Nicolae Teodorescu, talonați de cei mai tineri savanți din generația anilor dictaturii comuniste.
Contribuţii originale în sectoare “exotice” ale matematicii, aceea a lui Pius Servien (1902-1959), ca precursor pe plan mondial al esteticii matematice, şi a lui Matilda Ghyka (1881-1956), teoretician a ceea ce se numeste “numărul de aur” regăsit în operele de artă.
Propus de: CatanoiuDaniel1 | 10.12.2013 17:37
Matematicienii
Propus de: iulianasweety50 | 09.12.2013 18:28
Matematicienii
Propus de: iulianasweety50 | 09.12.2013 18:24
CONTRIBUŢII ROMÂNEŞTI LA DEZVOLTAREA ŞTIINŢEI ŞI TEHNICII











Propus de: No1serban | 03.12.2013 20:32


Comentarii (0)
Nu există niciun comentariu
Autentificaţi-vă pe site pentru a putea publica un comentariu.